Correlating stock returns using Python

August 2019

In this tutorial I'll walk you through a simple methodology to correlate various stocks against each other. We'll grab the prices of the selected stocks using python, drop them into a clean dataframe, run a correlation, and visualize our results.

(1) Import libraries, select our list of stocks to correlate

 import numpy as np
 import pandas as pd
 #used to grab the stock prices, with yahoo
 import pandas_datareader as web
 from datetime import datetime
 #to visualize the results
 import matplotlib.pyplot as plt
 import seaborn

 #select start date for correlation window as well as list of tickers
 start = datetime(2017, 1, 1)
 symbols_list = ['AAPL', 'F', 'TWTR', 'FB', 'AAL', 'AMZN', 'GOOGL', 'GE']

(2) Pull stock prices, push into clean dataframe

#array to store prices
symbols=[]

#pull price using iex for each symbol in list defined above
for ticker in symbols_list: 
    r = web.DataReader(ticker, 'yahoo', start)
    # add a symbol column
    r['Symbol'] = ticker 
    symbols.append(r)

# concatenate into df
df = pd.concat(symbols)
df = df.reset_index()
df = df[['Date', 'Close', 'Symbol']]
df.head()

We're now left with a table in this format:

date	close	symbol
2017-01-03	113.4101	AAPL
2017-01-04	113.2832	AAPL
2017-01-05	113.8593	AAPL

3) However, we want our symbols represented as columns so we'll have to pivot the dataframe:

 df_pivot = df.pivot('date','symbol','close').reset_index()
 df_pivot.head()

	date	AAL	AAPL	AMZN	F	FB	GE	GOOGL	TWTR
0	2017-01-03	45.7092	113.4101	753.67	11.4841	116.86	30.1370	808.01	16.44
1	2017-01-04	46.1041	113.2832	757.18	12.0132	118.69	30.1465	807.77	16.86
2	2017-01-05	45.3044	113.8593	780.45	11.6483	120.67	29.9754	813.02	17.09
3	2017-01-06	45.6203	115.1286	795.99	11.6392	123.41	30.0610	825.21	17.17
4	2017-01-09	46.4792	116.1832	796.92	11.5206	124.90	29.9183	827.18	17.50

(4) Next, we can run the correlation. Using the Pandas 'corr' function to compute the Pearson correlation coeffecient between each pair of equities

 corr_df = df_pivot.corr(method='pearson')
 #reset symbol as index (rather than 0-X)
 corr_df.head().reset_index()
 del corr_df.index.name
 corr_df.head(10)

symbol	AAL	AAPL	AMZN	F	FB	GE	GOOGL	TWTR
AAL	1.000000	0.235239	0.226061	0.068024	0.356063	-0.332681	0.494075	0.169487
AAPL	0.235239	1.000000	0.868763	0.184501	0.911380	-0.895210	0.903191	0.781755
AMZN	0.226061	0.868763	1.000000	0.108351	0.744732	-0.937415	0.864455	0.955373
F	0.068024	0.184501	0.108351	1.000000	0.206055	-0.216064	0.189753	0.161078
FB	0.356063	0.911380	0.744732	0.206055	1.000000	-0.814703	0.900033	0.650404
GE	-0.332681	-0.895210	-0.937415	-0.216064	-0.814703	1.000000	-0.882526	-0.866871
GOOGL	0.494075	0.903191	0.864455	0.189753	0.900033	-0.882526	1.000000	0.789379
TWTR	0.169487	0.781755	0.955373	0.161078	0.650404	-0.866871	0.789379	1.000000

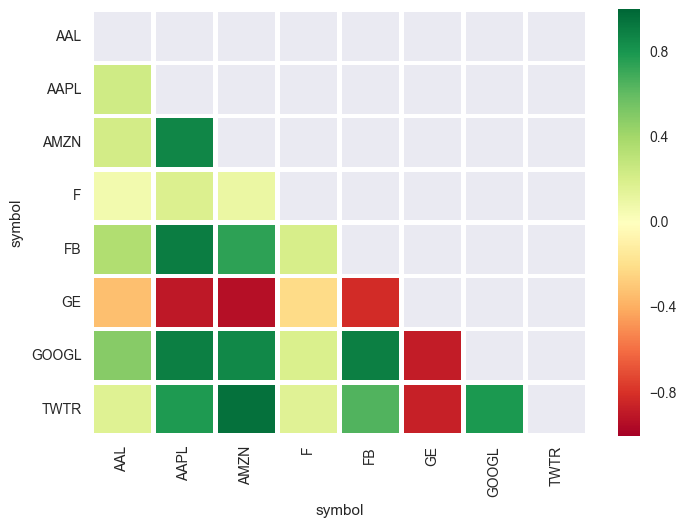
5) Finally, we can plot a heatmap of the correlations (with Seaborn and Matplotlib) to better visualize the results:

 #take the bottom triangle since it repeats itself
 mask = np.zeros_like(corr_df)
 mask[np.triu_indices_from(mask)] = True
 #generate plot
 seaborn.heatmap(corr_df, cmap='RdYlGn', vmax=1.0, vmin=-1.0 , mask = mask, linewidths=2.5)
 plt.yticks(rotation=0) 
 plt.xticks(rotation=90) 
 plt.show()

Here we can see that, as expected, the tech companies are generally pretty highly correlated (as indicated by dark green -- AMZN/GOOGL, FB/AAPL, etc). Conversely, Ford (F) and General Electric (GE) are either not correlated or negatively correlated with the rest of the group.