The smartest prep.
Tailored to your data interview.
No more guessing.
Prep smarter with a custom plan built around what
top companies actually test.
Built for Every Data Role
Personalized prep plans for Data Science, Engineering, ML, and Analytics.
Join a community of thousands of candidates who’ve landed jobs at top companies
Our platform
3 Steps to Smarter Interview Prep
Select the role and company you’re preparing to interview for.
Enter a company, role, or full job description — we’ll build around it.
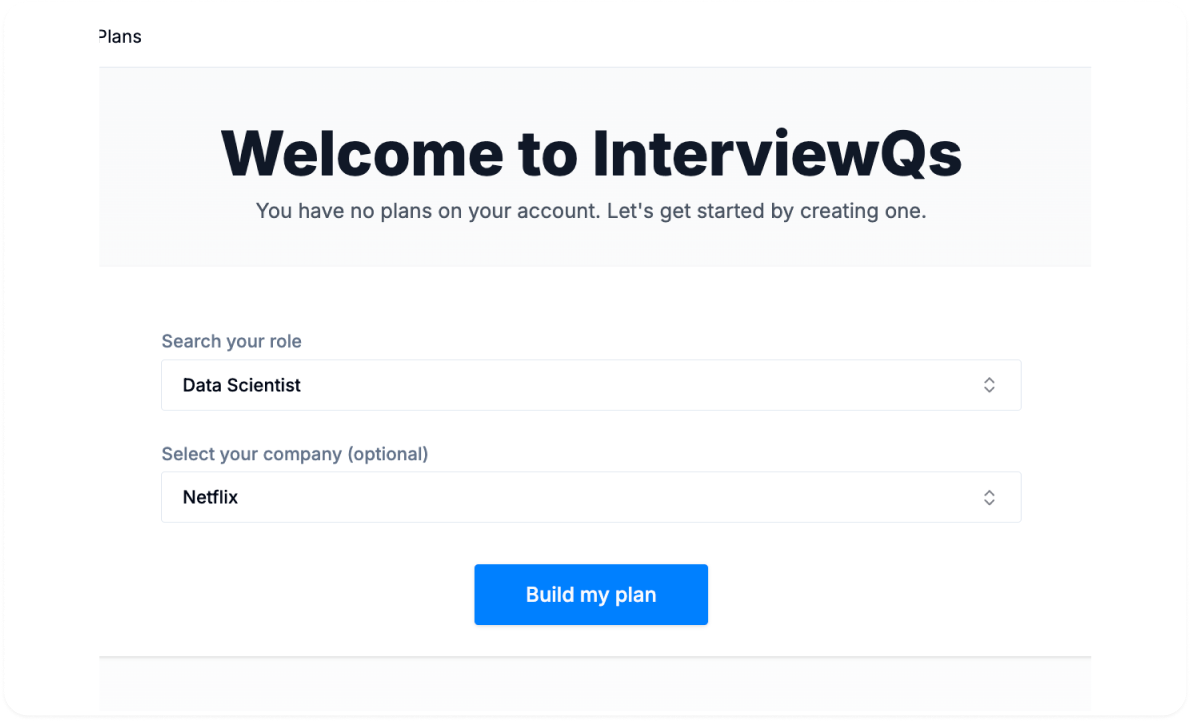
We’ll make you a customized plan.
We’ll make you a custom plan, tailored to focus on the skills you need to prepare for the interview.
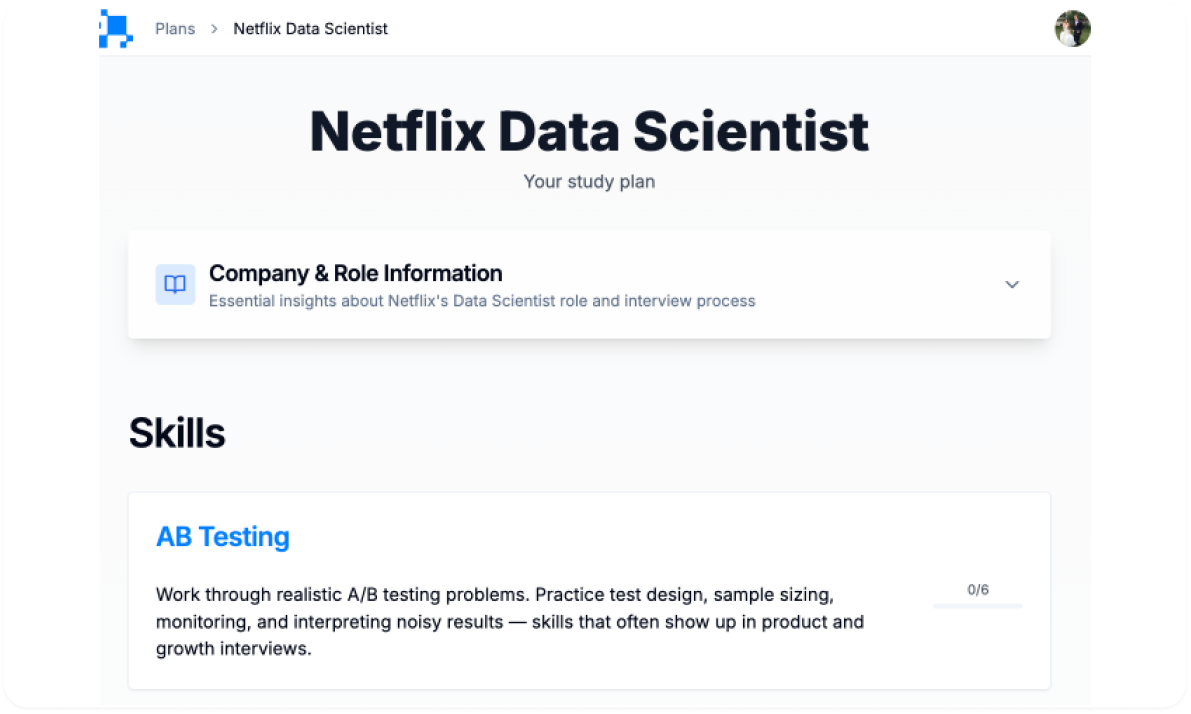
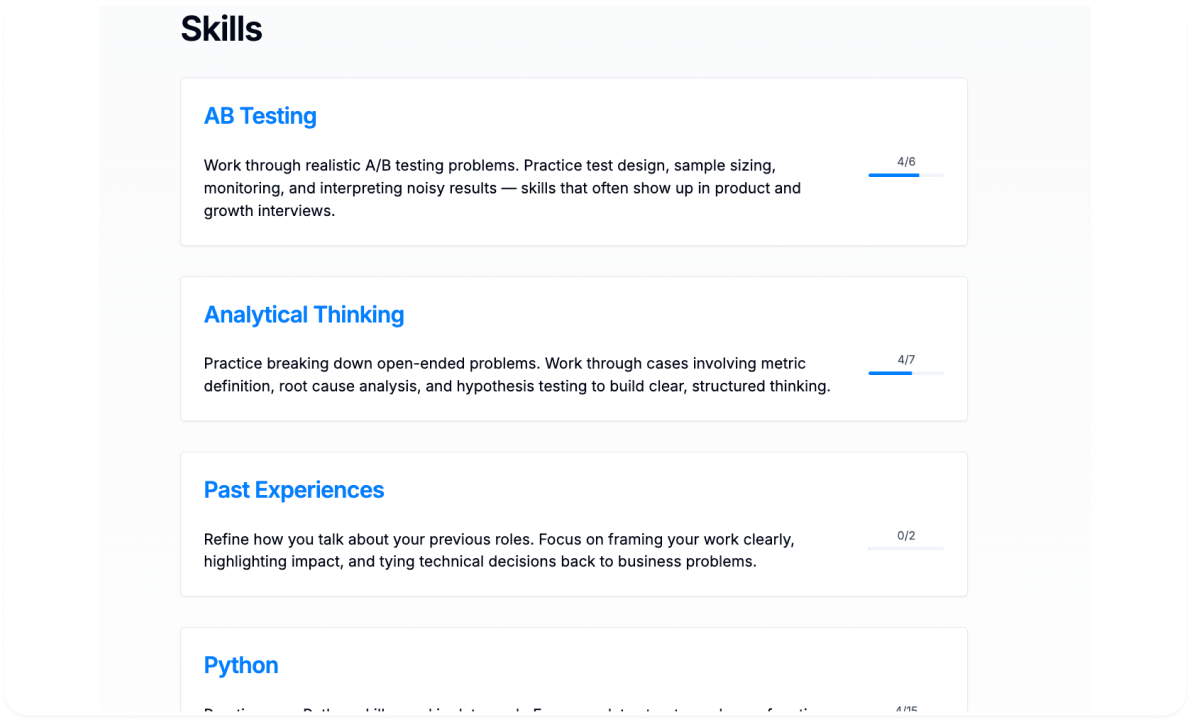
Prepare for your interview with InterviewQs
Use your custom plan to practice questions, review answers, and read up on tips for your interview.
See what others are saying
The majority of premium users (90%+) who canceled their subscription did so because they landed a job!
InterviewQs helped me cover all the basics of technical data science interviews, from SQL/Python to probability/statistics. The confidence/knowledge I gained from the service was incredibly useful, helping me land a data scientist position at Red Hat.
I've been on the mailing list since the initial beta, and found the questions to be very helpful with the technical side of my data science interview at Facebook, ultimately helping me land a role.
InterviewQs has been a great way to stay relevant with my data skills at Facebook, and has given me an edge in my Master’s Program in Data Science at Georgia Tech! It’s awesome to get a wide variety of questions and solutions sent to me on a regular basis.
Used by thousands of students and industry workers
